The Mathematics of a Fair Fantasy Sports Trade
Introduction
We are now rapidly approaching the major league trade deadline of July 31. In our own fantasy baseball leagues, we often try to mimic real-life – and trading is no different. We set up an arbitrary date in the 2nd half of the baseball season, in which we agree to cease trading with our league mates for the remainder of the season.
Some leagues set their internal deadline a few days following the major league one. Some leagues set the deadline to be the All-Star game. Whatever your league’s trade stopping point may be, the idea is to prevent last minute unfairness or possible collusion. As a natural byproduct, having that set date often sparks some league excitement in the waning trading hours!
The title of this article is, The Mathematics of a Fair Fantasy Trade. Often, leagues will allow its individual team members (or commissioner) to vote upon and potentially veto a trade which they deem as “unfair.” These leagues will often state in their constitutions ideas resembling:
All trades should be “fair.” A trade does not necessarily need to be “good” for both sides.
The above verbiage is taken verbatim from the constitution of one of my home leagues. For a number of my other leagues, their bylaws also state something similar. League guidelines often emphasize the notion that fair trades aren’t necessarily good for both sides. They claim that a fair fantasy baseball trade does not necessarily have to be a good one.
I completely disagree with that premise. The truth is that they are one and the same. Any trade that is good for both sides is a fair one. Any trade that is fair, has the realistic potential to benefit both teams.
Before continuing any further, I want to deal with a common point of contention regarding (the fairness of) trades. Most players like to argue that “no trades should ever be vetoed” – that if two consenting adults agree to swap players in the middle of a season, they should be allowed to do so. The premise of this argument is centered upon the notion that unless collusion is otherwise suspected – fairness is not to be considered. All trades should stand.
This article will not debate that point in either direction. I am not here to opine on league etiquette. Instead, I wish to attempt to put forth some measurable principles for what constitutes a “fair” trade.
So how can we mathematically quantify what makes a fantasy sports trade fair?
Fairness in Reinsurance
For those of you who do not know my professional background – I am a certified actuary. I am a Fellow of both the Casualty Actuarial Society and the Society of Actuaries.
In a nutshell, an actuary is an insurance professional who is well versed in the mathematics of insurance. Actuaries price insurance contracts, decide on the amount of reserves that companies need hold for claims, inform management on the ROEs of various lines of business, and deal with many other assorted insurance related tasks.
At my company, a large area of focus for me these days is the area of reinsurance. Reinsurance very simply, is insurance for insurance companies. One company who might hold too much risk, looks to layoff (for a price) part of their risk to another insurance company who wants to take on more [risk]. To diversify, my company both buys and sells reinsurance.
Today, I will attempt to draw upon my knowledge of the insurance world to help formulate principles of what constitutes a fair trade in fantasy sports.
One law/statute pertaining to reinsurance, is that a reinsurance transaction must be a fair one. In fantasy sports, our concern often lies with trades that appear to be lose-lose ones, i.e. that the potential swap may categorically cause harm to a particular team. In insurance, regulators are concerned with the opposite side. The law focuses on preventing reinsurance transactions from being a win-win for any one party; trading companies must demonstrate that they are subject to a plausible downside.
Let’s take a look at the verbiage of what constitutes a fair reinsurance transaction:
“It is reasonably possible that the reinsurer may realize a significant loss from the transaction.”
This statute is taken directly from the Statement of Statutory Accounting Principles used by the National Association of Insurance Commissioners (SSAP 62R). To illustrate fairness of the transaction, the appointed actuary would have to demonstrate that the ceding company is at risk to lose money, and with a significant probability of that occurring.
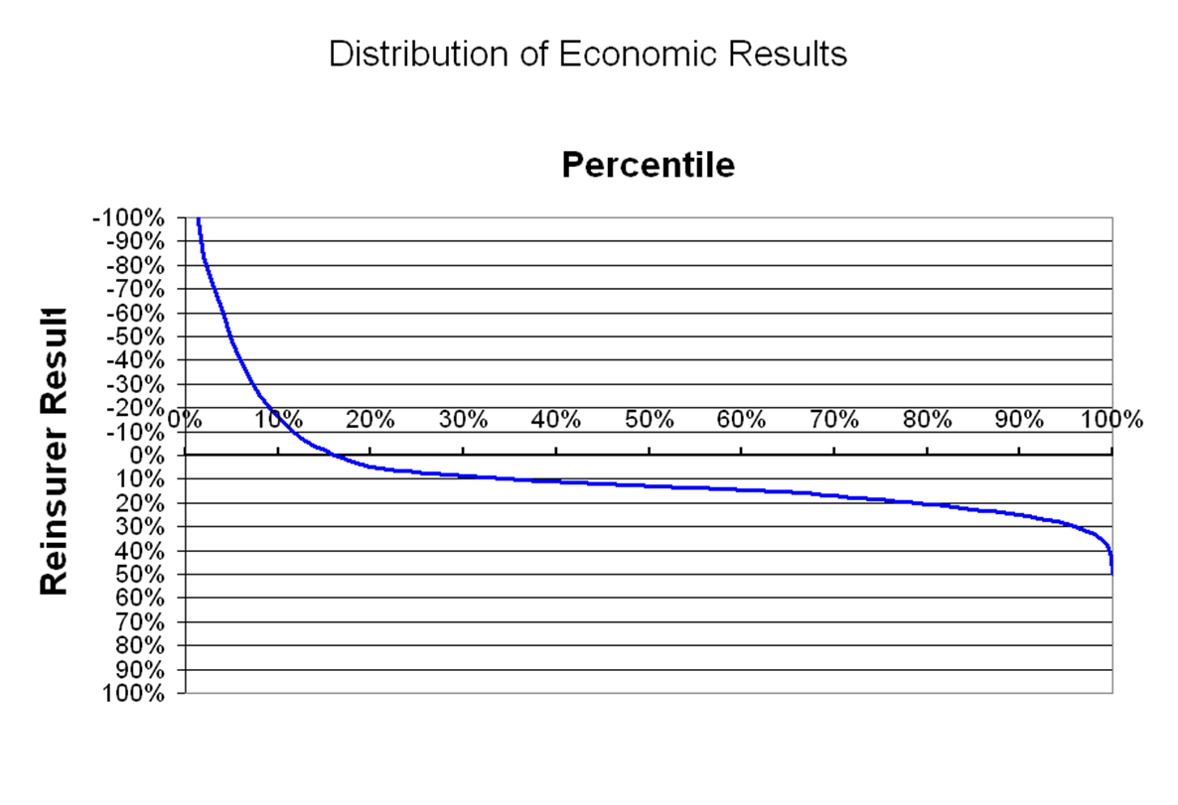
Without getting too technical with insurance terms, the above is a graph that I would potentially put together for regulators. The graph displays the resulting analysis of a particular reinsurance transaction.
- The X-Axis displays the percentiles. The worst possible outcomes are on the left-hand side, and the best outcomes are displayed to the right. The 50% mark would be the median scenario outcome.
- The Y-Axis displays the reinsurer results. The favorable outcomes (where the company makes money) are towards the bottom, and the unfavorable outcomes are towards the top. A 0% reinsurer result means that the company broke even for the year.
To test if one is reading the graph correctly, note the following relevant data points:
- 15% of the time, the company loses money. A 0% reinsurer result is modeled at the 15th
- 50% of the time, the company makes at least a 13% profit. A 13% reinsurer result is modeled at the median.
So, regarding resinurance:
What mathematically constitutes a fair reinsurance transaction?
Although there are a number of actuarial methods to answer this question, I will share one commonly used method which can easily be identified and verified on the graph. It is known as the 10-10 Rule.
The 10-10 Rule:
There must be at least a 10% probability that the reinsurer will realize at least a 10% loss.
Looking at the above chart:
- There is a 12% chance that the reinsurer will lose 10%.
- There is a 10% chance that the reinsurer will lose 17%.
Since the 10-10 Rule has been satisfied, this reinsurance transaction may be deemed fair, or in this case – legal.
Fairness in Fantasy – Example: Game 162
Let’s jump back to fantasy sports. Once again, in fantasy – we are concerned not with illustrating the downside of a trade – but in how each team may profit. To mimic the insurance world, what needs to be demonstrated is that a trade provides the circumstances for a reasonably possible significant upside.
Let’s start with an exaggerated case. Suppose that there is only one game left before the season ends. You are playing in a 10 team 5×5 mixed roto redraft league, where the top 3 finishers get paid out. Here are the current rotisserie standings:
| Place | Team | Points |
|---|---|---|
| 1 | Team A | 78.5 |
| 2 | Team B | 77.5 |
| 3 | Team C | 71 |
| 4 | Team D | 71 |
| 5 | Team E | 62 |
| 6 | Team F | 59.5 |
| 7 | Team G | 48 |
| 8 | Team H | 41 |
| 9 | Team I | 29.5 |
| 10 | Team J | 12 |
Suppose that there is no trade deadline in this league. Team J would like to make a trade with Team B. Without even knowing which players would be traded, I can state without any hesitation that any trade would be unfair.
Why?
It doesn’t take a deep mathematical understanding to realize that Team J is so far removed from the money that even if they trade their three worst players for Team B’s three best players, they would still have no shot at winning any prize money. For instance, Team J could trade Matt Harvey, Sean Gilmartin and Bubba Starling for Mike Trout, Mookie Betts and Christian Yelich – and yet they would still not be able to amass enough points to propel them to a money finish.
Numerically, Team J’s expected value of winnings prior to a trade is $0 (their probability of winning money is 0%). Following any trade, Team J’s expected value of winnings would still be $0 (0% chance of winning money). Team J has a 0% chance of gaining from the trade.
The key here is not to look at the specific players involved in the trade in a vacuum. The context matters in terms of the reasonably possible chance for a gain. This trade is unfair because the probability of Team J winning money improves by 0%. It starts at 0% and it ends at 0%. There is no reasonable chance for gain here.
Fairness in Fantasy – Example: Arenado for Engel
Consider the following trade: Nolan Arenado for Adam Engel
Would this be considered a fair trade?
Let’s see some statistical information before we attempt to answer the question:
| Player | Perspective | BA | R | RBI | HR | SB |
|---|---|---|---|---|---|---|
| Nolan Arenado | 2018 Stats | .297 | 104 | 110 | 38 | 2 |
| Nolan Arenado | 2019 ATC Projections | .294 | 101 | 114 | 39 | 2 |
| Player | Perspective | BA | R | RBI | HR | SB |
|---|---|---|---|---|---|---|
| Adam Engel | 2018 Stats | .235 | 49 | 29 | 6 | 16 |
| Adam Engel | 2019 ATC Projections | .217 | 47 | 30 | 8 | 15 |
Above are the 2018 final stats, plus the original 2019 ATC projections for both Arenado and Engel. The statistical difference between the two players can be summarized by:
| Player | Perspective | BA | R | RBI | HR | SB |
|---|---|---|---|---|---|---|
| Arenado vs Engel | 2018 Stats | +.062 | +55 | +81 | +32 | -14 |
| Arenado vs Engel | 2019 ATC Projections | +.077 | +54 | +84 | +31 | -13 |
[Positive/Blue values indicate statistics in Arenado’s favor. Negative/Red values indicate statistics in Engel’s favor.]
Before you decide on the fairness of the trade, let’s take a quick look at where each player was drafted in the 2019 pre-season:
| Player | 2019 Draft Round |
|---|---|
| Nolan Arenado | 1 |
| Adam Engel | Undrafted |
So, would this be considered a fair trade?
From a pure valuation point of view, the two seem rather distant in fantasy value. In a vacuum, it is hard to fathom a fair trade involving the two players.
But my answer is that I don’t know. There isn’t enough information to answer the question. I can’t answer without knowing the context. One cannot tell if this trade will result in a reasonable chance at a gain, unless we know when the trade was made, the current league standings, and the composition of the teams in question.
Fairness in Fantasy – Categorical Gains
For the above trade of Arenado for Engel, consider the following example of a 5-team, 5-category rotisserie league (offense only). The top two teams at the end of the season will get paid out prize money. The Giants, who have Nolan Arenado on their squad have offered him up for Adam Engel who is currently on the Padres.
Here are the current league statistics and standings (hypothetically) as of August 25:
| Fantasy Team | BA | R | RBI | HR | SB |
|---|---|---|---|---|---|
| Rockies | 0.268 | 794 | 740 | 242 | 83 |
| Dodgers | 0.273 | 785 | 735 | 241 | 82 |
| Giants | 0.251 | 720 | 801 | 300 | 81 |
| D-Backs | 0.272 | 790 | 737 | 230 | 78 |
| Padres | 0.267 | 788 | 731 | 227 | 79 |
| Fantasy Team | BA | R | RBI | HR | SB | Total Points |
|---|---|---|---|---|---|---|
| Rockies | 3 | 5 | 4 | 4 | 5 | 21 |
| Dodgers | 5 | 2 | 2 | 3 | 4 | 16 |
| Giants | 1 | 1 | 5 | 5 | 3 | 15 |
| D-Backs | 4 | 4 | 3 | 2 | 1 | 14 |
| Padres | 2 | 3 | 1 | 1 | 2 | 9 |
Let’s evaluate the “fairness” of the trade from the point of view of the Giants. Let’s look into the potential gains/losses for the individual categories.
- Batting Avg. – The Giants are far behind the pack. They realistically do not stand to lose or gain any points in batting average.
- Runs – The Giants are far behind the pack. They realistically do not stand to lose or gain any points in runs.
- RBI – The Giants are far ahead of the pack. They realistically do not stand to lose or gain any points in RBI.
- HR – The Giants are far ahead of the pack. They realistically do not stand to lose or gain any points in HR.
- SB – The Giants are right in the middle of the pack. They can gain 2 points, or they can lose 2 points over the final few weeks of the season.
Despite the fact that Arenado should outperform Engel in BA, R, RBI & HR – The Giants will not lose or gain any points in any of the 4 scoring categories. They are either far ahead or far behind in each and will stay at the same point total regardless. But by acquiring Engel, who should outperform Arenado in SBs – the Giants will now be more likely to gain SB points rather than to lose them.
The Giants are greatly aided by trading Arenado for Engel. In this particular situation, Engel is worth more to the Giants. Not only is there a very reasonable chance that they can gain points – the Giants are expected to gain points.
This was quite an extreme example. Four categories were well out of reach in either direction. But suppose that the RBI and Runs categories would have been closer, with the Giants somewhere in the middle of the pack in each. Let’s evaluate the same trade in this alternate context.
| Fantasy Team | BA | R | RBI | HR | SB |
|---|---|---|---|---|---|
| Rockies | 0.271 | 795 | 752 | 242 | 82 |
| Dodgers | 0.268 | 791 | 749 | 241 | 79 |
| Giants | 0.257 | 780 | 747 | 300 | 77 |
| D-Backs | 0.269 | 743 | 696 | 230 | 80 |
| Padres | 0.272 | 742 | 693 | 240 | 78 |
| Fantasy Team | BA | R | RBI | HR | SB | Total Points |
|---|---|---|---|---|---|---|
| Rockies | 4 | 5 | 5 | 4 | 5 | 23 |
| Dodgers | 2 | 4 | 4 | 3 | 3 | 16 |
| Giants | 1 | 3 | 3 | 5 | 1 | 13 |
| D-Backs | 3 | 2 | 2 | 1 | 4 | 12 |
| Padres | 5 | 1 | 1 | 2 | 2 | 11 |
Here in this example, the loss of Arenado might hurt the Giants in two categories – whereas the gain of Engel would only help in one category.
Let’s ask the question once again:
Is this a fair trade?
Think Probabilistically
My actuarial hat returns.
Let’s think about the current context not in terms of rotisserie points – but in probabilistic terms. To this end, I have modeled the following to help us evaluate each team’s winning propensity:

Currently, I estimate that the Giants have a 3.6% chance of finishing in 1st place and a 32.9% chance of landing in the money (finishing in the top 2). These odds arise from taking the current accumulated team statistics, projecting the expected rest of season (ROS) team statistics, simulating 1000 possible ROS outcomes, and then quantifying the results.
My method is quite complicated and heavily actuarial. It involves Monte Carlo simulations, understanding the inherent statistical volatility per stat, correlating the categories, and smoothing results. Perhaps I will write more about this procedure at a later time.
Let’s look at a visual. Below is the point density table per team for each of the possible end of season point totals. The percentages are the probabilities that a given team will end up with the corresponding point totals.

You can quickly see that the Padres, though currently in last place – have a higher point total upside than the D-Backs. Currently, the Giants have the smallest volatility of final results.
In order to opine on the fairness of the trade, we need to look at the results for the Giants (and the Padres) after they swap Arenado for Engel. To evaluate:
- I added the rest of the season stats of Engel to the Giants, and subtracted Arenado’s ROS stats.
- I added Arenado’s ROS stats to the Padres, and subtracted Engel’s ROS stats.
- I then re-ran my model.
Below are the results, and the derived changes:


Both the Giants and the Padres expect (on average) to gain points as a result of the trade. The Giants improve by 0.3 points, and the Padres improve by 0.4 points. More importantly, their probabilities improve. Both the Giants and the Padres increase their probability of winning AND their probability of being “in the money.” The Giants go from a 32.9% chance of cashing out to a 34.1% chance. It might seem small – but nonetheless, the trade is modeled as accretive. The trade is a net positive on a probabilistic basis for both of the trading partners … which is how it should be.
To see the effect of the trade from a visual perspective, I have also compiled the change in exceedance probabilities as a result of the trade. This chart differs slightly from the one above; the probabilities displayed below are the net change per team of (meeting or) exceeding the corresponding point thresholds.
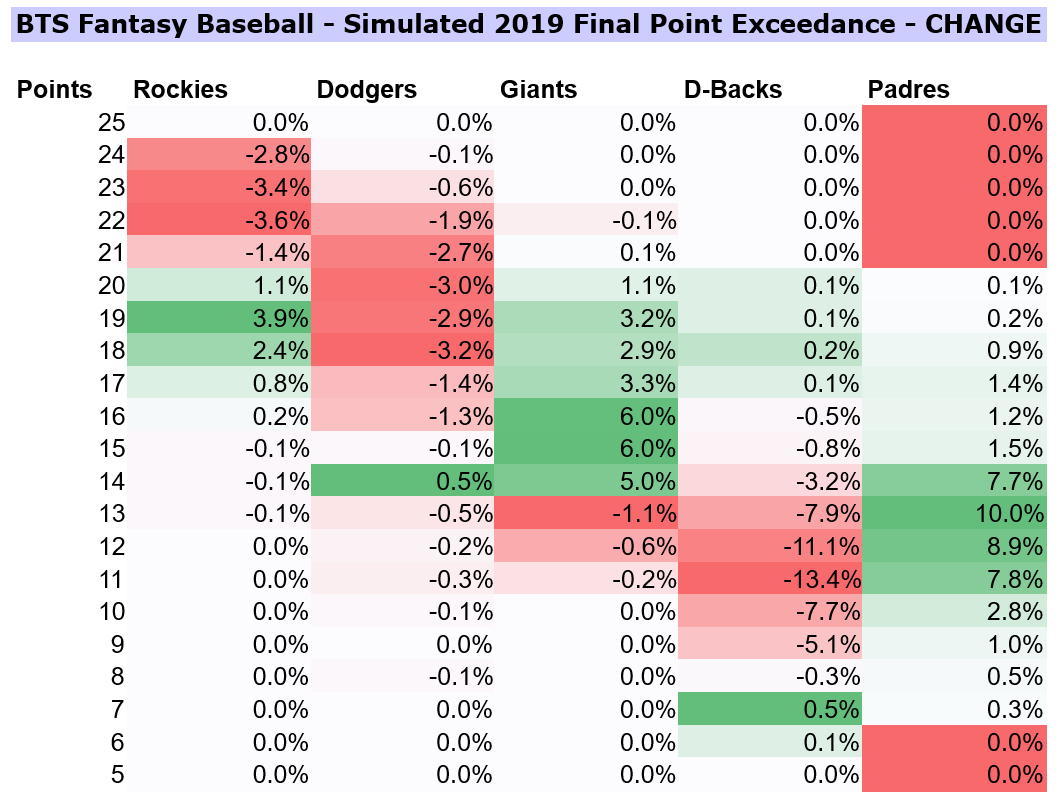
This is a fantastic chart, because it allows us to look at the change in the resulting distribution of each team.
- For the Giants, the top of their graph is drenched in green, which means that they have increased their upside. The bottom part of their graph has some reds, which means that they have also capped their downside.
- For the Padres, the top stretch of the graph is red, which means that they have lowered their upside for achieving 21+ points. However, the entire middle section is green – which signifies that they have improved their odds for most attainable point thresholds.
- The Rockies have a mixed bag. On one hand, their upside of 21+ pts. is capped. At the same time, the 16 to 20 point range has now grown – which would likely be “in the money” range.
- Poor Dodgers! They seem to be the biggest losers of this trade, declining in probability exceedance at almost every single point threshold.
Is this a fair trade?
We have demonstrated that both the Giants and Padres have a significant chance to improve their odds of winning. Given the mathematical, actuarial and probabilistic evidence above, the answer is a resounding … YES.
Conclusion
Running Monte Carlo simulations and generating probabilities of exceedance is a rather complex process. Either is certainly not needed in order to opine on the fairness of a trade. What I wanted to impart to you today was simply to consider that fairness is quantifiable. You can mathematically state what a good trade should entail.
Furthermore, a trade can and should be beneficial for both parties. A trade might increase a team’s risk. It might lower a team’s expected point total, but it may also be able to provide more tail scenarios for profit (i.e. more upside). As long as one can reasonably conceive the scenarios where each team can not only gain – but can jump “into the money,” then the trade would be a fair one.
Hopefully, this discussion did not only give you the intended insights – but it will also make you a better trading partner in the long run.
Ariel is the 2019 FSWA Baseball Writer of the Year. Ariel is also the winner of the 2020 FSWA Baseball Article of the Year award. He is the creator of the ATC (Average Total Cost) Projection System. Ariel was ranked by FantasyPros as the #1 fantasy baseball expert in 2019. His ATC Projections were ranked as the #1 most accurate projection system over the past three years (2019-2021). Ariel also writes for CBS Sports, SportsLine, RotoBaller, and is the host of the Beat the Shift Podcast (@Beat_Shift_Pod). Ariel is a member of the inaugural Tout Wars Draft & Hold league, a member of the inaugural Mixed LABR Auction league and plays high stakes contests in the NFBC. Ariel is the 2020 Tout Wars Head to Head League Champion. Ariel Cohen is a fellow of the Casualty Actuarial Society (CAS) and the Society of Actuaries (SOA). He is a Vice President of Risk Management for a large international insurance and reinsurance company. Follow Ariel on Twitter at @ATCNY.

….which all goes out the window if there’s even the slightest consideration of multi-year strategy. Even in a redraft league where next year’s draft order is based on the prior year’s finish an “unfair” trade may help the “harmed” team later.
Not to mention that the math becomes meaningless when owners simply choose not to belief projections, or when two different owners’ projections disagree.
On the contrary for multi-year. The principles still apply, but the math gets more complicated, as you are looking at expected payouts over multiple years, etc.
While absolutely true in a technical sense, I don’t think very many people would buy that. If your Team I sells all of it’s good players to Team B in a deliberate effort to finish behind Team J and obtain a higher draft pick in the next year, a LOT of people would cry foul.
…which gets back to almost never vetoing trades. Once you’re in the business of judging someone else’s trade, all you’re really judging is to what extent it hurts you.
Depends on what the probabilistic gain is on the higher draft pick the following year. If it is a 0.1% gain, then that’s not significant. If its a 1.5% gain in expected winnings, then it is.
One better draft pick slots aren’t worth that much, but if we are talking some current prize money for a 10th vs 11th finish, then it is!
The principle still holds as to fair = chance for significant gain.